Gráficos de Barras en la Estadística
Un gráfico de barras es aquella
representación gráfica bidimensional en que los objetos gráficos elementales son un conjunto de rectángulos dispuestos
paralelamente de manera que la extensión de los mismos es proporcional a la
magnitud que se quiere representar.
Los rectángulos o barras pueden estar
colocados horizontal o verticalmente. En éste último caso reciben también el
nombre de gráficos de columnas.
En lo siguiente hablaremos indistintamente de ellos
como "gráficos de barras"
Como También pueden haber Gráficos de Columnas
Típicamente se utilizan para
comparar magnitudes entre varias categorías o
la evolución en el tiempo (el cambio) de una determinada
magnitud.
la comparación de la evolución en el tiempo de
varias categorías, esto es, se suelen
usar también para la mezcla de las dos utilidades anteriores.
ipos de Datos
Como sabemos hay tres tipos de datos
Categóricos, también llamados Nominales (pájaros, mamíferos,
altos, bajos, verdes o azules)
Ordinales o Secuenciales (el
abecedario, los meses del año)
Cuantitativos o Numéricos (cualquier
cosa que se pueda representar con números)
Las variables de datos principalmente usadas en los gráficos de barras son
las de tipo categórico y
las ordinales (especialmente
las temporales).
Este tipo de representación no es muy apropiada para representar datos cuya
variable sea cuantitativa.
Cuantitativo
Un eje cuantitativo con una escala lineal que sirve de
referencia a la magnitud de la variable en cuestión. En un gráfico de columnas
éste es el eje de ordenadas en y en uno de barras es el eje de abscisas x Este
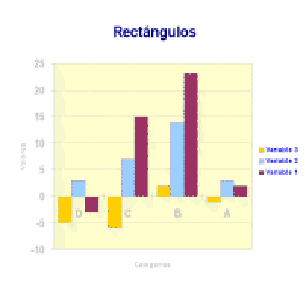
eje puede contener valores negativos. como lo ejemplifica la imagen siguiente.
Categórico u Ordinal
Un eje categórico u ordinal en el que se disponen
las categorías o los elementos de la secuencia (el eje de abscisas x en un
gráfico de columnas o el de ordenadas y en un gráfico de barras). Este eje es
perpendicular al cuantitativo. como lo ejemplifica la imagen que coloque para mas explicación
Conjunto de rectángulos
Un conjunto de rectángulos cuya extensión
paralela al eje cuantitativo es proporcional a la magnitud de la categoría o
secuencia representada en el ejemplo siguiente
Tipos principales de gráficos de barras
Existen muchos tipos y variantes de los mismos,
discutiremos aqui algunos de los más relevantes. como lo son
Sencillo
Contiene solamente una serie de datos por
ejemplo, las ventas en distintos meses en un mismo país
Agrupados
Contiene varias series de datos, por
ejemplo las ventas mensuales en varios países. En este caso el eje secuencial
contendría los meses y el cuantitativo la cifra de ventas. Cada serie de datos
se representa mediante un conjunto de rectángulos que comparten color o
textura.
En cada categoría o secuencia los rectángulos suelen estar juntos, formando un
grupo, mientras que entre grupos se deja un espacio. Así en el ejemplo de las
ventas, los resultados obtenidos por Francia, Inglaterra e Italia en el mes de
noviembre se representarían como tres rectángulos de alturas proporcionales a
su valor colocados lado a lado en el espacio dejado en el eje secuencial para
el mes de noviembre.
Por: Santos Mauricio Orozco Agustín